市面上常用的Oscillator產品基本上都來源于國外進口,不僅分類眾多,規格與參數也時常讓人頭疼,對于不熟悉頻率元件的采購來說,常常不知如何選擇合適匹配的晶體振蕩器.在此建議可以先咨詢工程,如工程也不清楚的,可以向供應商獲取相關的產品資料,給工程技術參考對應.Oscillator產品規格書里通常都會備注,該系列適用于哪些產品,因為晶體振蕩器制造商在生產之前,都會設計好產品的制造方案,匹配不同的電子或智能產品.
石英晶體是具有壓電特性的機械諧振器.壓電特性(晶體上的電勢與機械變形成比例)允許它們用作電路元件.晶體由于其高品質因數(QF),優異的頻率穩定性,嚴格的公差和相對低的成本而被廣泛用作振蕩器中的諧振元件.本教程介紹了使用AT切割晶體設計簡單晶體振蕩器時要解決的主要設計注意事項.描述了晶體振蕩器的基本特性以及可能影響其在各種應用中的性能的因素.這里討論的主題是對ISM頻段無線電十年設計和應用中遇到的問題的匯編.這些主題包括負載電容.
水晶模型的基礎知識
石英晶體被電模擬為與并聯電容并聯的串聯RLC分支(圖1).RLC分支系列(通常稱為運動臂)模擬壓電耦合到機械石英晶體諧振器.并聯電容表示由電極金屬化的平行板電容和雜散封裝電容兩者形成的物理電容.

圖1.基模石英晶體的簡單電氣模型.

圖1所示的模型適用于基本模式操作.類似的模型也適用于晶體諧振器的泛音操作.泛音模型包括與圖1中所示元件并聯的附加串聯RLC分支.附加泛音RLC串聯分支具有接近基本串聯諧振頻率的奇數倍的諧振頻率.對于工作在基頻模式,頻率范圍為5MHz至30MHz的石英水晶振子,電路元件的典型值為:
C12fF至20fF(動態電容)R110Ω
至150Ω(等效串聯電阻,ESR)
L1由C1和工作頻率(動態電感)決定
C00.5pF至5pF(并聯電容)
其中運動元素是機械共振的電學模擬和晶體的壓電性質.ESR模擬機械共振的損失,對于沒有外部驅動電壓的串聯RLC電路,所有電壓的總和產生以下微分方程:
L×dI/dt+I×R+(1/C)×∫I×dt=0
根據定義,我可以用dQ/dt替換,產生:
L×d²Q/dt²+R×dQ/dt+Q/C=0
要么
d2Q/dt²+(R/L)×dQ/dt+Q/(L×C)=0
這是形式d2Q/dt²+(ω的0/QF)×DQ/DT+Q×ω02=0.
這產生對RLC電路的公知的結果:自然頻率,ω0,是電感和電容的乘積的倒數的平方根.

圖2.晶體機械模型.

晶振的力學模型由質量組成;彈簧具有相關的彈簧模量或剛度;以及緩沖模型(圖2).施加在晶體上的力,忽略由于重力引起的固定力和空間偏移,導致質量加速(牛頓第二運動定律).在簡單線性模型,彈簧力和摩擦力中假設兩種力.彈簧力由胡克定律給出,F=K×Y,其中K是彈簧模量,Y是平衡位移.假設摩擦損失與緩沖器中柱塞的速度和緩沖器的摩擦常數D成比例.等同于這些力(沒有外部驅動力)給出:
M×d²Y/dt²+D×dY/dt+K×Y=0
要么
d²Y/dt²+(D/M)×dY/dt+Y×(K/M)=0
這是形式d²Y的/dt²+(ω0/QF)×DY/dt的+Y×ω02=0.
由此產生的機械系統固有頻率必須等于電氣系統的固有頻率.這會產生:
ω0=√(1/(L×C)=√(K/M)

圖3.立方石英諧振器.頂面和底面上的電極,A=L×W.

在最窄尺寸的相對面上具有電極金屬化的立方形或圓柱形石英諧振器的質量與電極面積和電極之間的間隔(即,最窄的尺寸或厚度)的乘積成比例,如圖3.
M~A×T.其中A是電極面積,T是厚度.相同立方形石英諧振器的彈簧模量與電極面積和厚度的倒數的乘積成比例.
K~A/T.由此,機械系統的固有頻率與電極面積無關,并且與厚度的倒數成反比:
ω0=√(K/M)?√(A/(T×A×T)=√(1/T2)=1/T
在許多可能的晶體諧振器選項中,AT切割晶體因其溫度系數特性和制造可重復性而廣受歡迎.對于AT切割石英晶振,機械共振是剪切模式,如圖4所示.在這種操作模式中,重心垂直和水平移動.因此,前面的分析是一維近似,可用于定性理解AT切割晶體的機械共振.

圖4.AT切割厚度,剪切模式共振.

從并聯電路的角度來看,晶體的總電阻抗將與電極面積成反比,因為較大的電極面積相當于多個較小的電極面積晶體并聯.因此,串聯電阻和動態電感將與電極面積成反比;并聯電容的運動電容和平行板部分將與電極面積成比例.并聯電容和運動電容具有線性關系,因為它們都與未封裝晶體的電極面積成比例,通常稱為晶體空白.如果封裝的寄生并聯電容可忽略不計,并且并聯電容平行板邊緣場可忽略不計,則該關系將成比例.
以下是基于前面分析的設計權衡清單:
較小的晶體電極區域對于較低的成本和可能較小的封裝尺寸是有吸引力的.但是,這個較小的區域會增加串聯電阻,從而減慢啟動時間(參見下面的啟動時間部分)并可以防止振蕩.較大的晶體電極區域較低的串聯電阻.但是,這個較大的區域會增加并聯電容,從而降低有源電路的負電阻(參見下面的負電阻部分),這反過來也會減慢啟動時間并防止振蕩.較大的無源諧振器電極面積增加了運動電容.由于外部電容性負載或頻率“拉動”,運動電容越大,對頻移的靈敏度越大.
負載電容
許多晶體振蕩器在晶體的并聯諧振點和施加的負載電容下工作.負載電容定義為晶體封裝外部的有效電容,施加在晶體的端子之間,如圖5所示.晶體制造商指定給定的負載電容以及操作頻率.負載電容與制造商指定的負載電容不同的操作會導致相對于制造商指定頻率的振蕩頻率誤差.頻率誤差是由于晶體的電容“拉”引起的.這可以通過將并聯和負載電容并聯組合,然后將該總和并聯負載電容與運動電容串聯組合來形成整體有效電容來證明.
C EFF=C MOTIONAL×(C LOAD+C SHUNT)/(C LOAD+C SHUNT+C MOTIONAL)

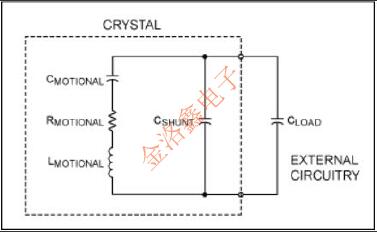
圖5.負載電容.

電容的總體有效變化非常小,因為運動電容通常比分流和負載電容低約三個數量級.因此,(C LOAD+C SHUNT)/(C LOAD+C SHUNT+C MOTIONAL)幾乎為一,并且有效總電容非常接近運動電容的值.請注意,隨著負載電容變大,(C LOAD+C SHUNT)/(C LOAD+C SHUNT+C MOTIONAL接近單位,并且負載電容的絕對變化對整體有效電容的影響減弱(較低的頻率牽引).以相同的方式,對于任何給定的負載電容,較小的運動電容也降低了頻率牽引,因為(C LOAD+C SHUNT)/(C LOAD+C SHUNT+C MOTIONAL)接近于單位.有關典型石英晶體的頻率與負載電容(牽引曲線),請參見圖6.

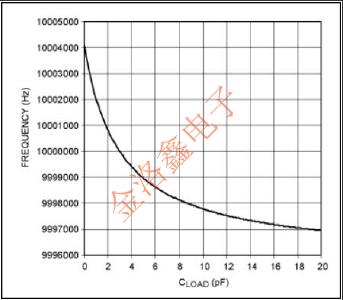
圖5FF為Ç6.典型牽引曲線運動,3pF的ÇSHUNT,3pF的聲明了cLOAD,10MHz的晶體.

負阻力
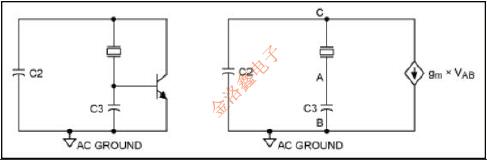
Pierce或Colpitts拓撲振蕩器通常與晶體結合使用以生成時間或頻率參考.兩種拓撲結構都被稱為“三點振蕩器”.一般形式如圖7和8所示.注意,除了AC接地點之外,兩個拓撲中的三個點A,B和C是相同的.

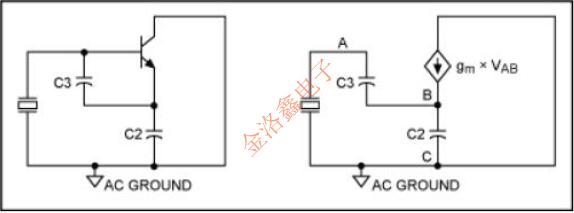
圖7.Colpitts振蕩器.

圖8.皮爾斯振蕩器.

虛假模式
不希望的機械共振通常存在于基頻附近.這些“寄生模式”可以被建模為與所需基頻RLC分支并行的附加串聯RLC分支,其方式與建模泛音操作的方式相同.寄生模式比期望模式具有更大的損耗(振蕩的機會更小);它們通常不會引起晶體振蕩器問題,除非它們損耗非常低或者有源電路非常微弱.通常,晶振廠家測試雜散模式,并且不會在寄生諧振頻率下發送具有低損耗(即,更大的振蕩機會)的單元.
具有大負電阻的石英水晶振蕩子通常在大多數振蕩周期期間限制或削減.在限制期間,電路的有效增益幾乎為零.因此,寄生模式不具有振蕩所需的增益,并且被所需的大信號振蕩有效地阻塞.在具有較低負電阻的一些情況下或具有軟限制的電路中,在整個期望的振蕩周期期間存在足夠的增益以支持二次不期望的振蕩.由此產生的多次振蕩共存會對PLL和其他電路中的相位頻率檢測器造成嚴重破壞.本文介紹了簡單晶體振蕩器的主要設計注意事項.與其他類型的無線電系統相關的主題,例如晶體振蕩器電路的相位噪聲,不是ISM無線電的限制因素,因此不予討論.

正在載入評論數據...

上一篇：如何用石英晶體保持時間穩定和精準

下一篇：RTC模塊使用MEMS Oscillator有哪些好處?

此文關鍵字： Oscillator設計晶體振蕩器基礎知識 AT切割石英振蕩子

精品国产一区二区三区不卡,日本一道高清不卡免费,国产一区二区三区久久精品,奇米4444,啊嗯啊羞羞免费视频,大色虫成人午夜在线观看

資訊中心

金洛博客

設計Oscillator基礎知識與注意事項

相關資訊

姓名：
郵箱：
正文：